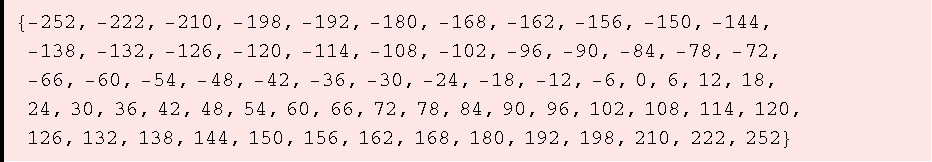Übung Algorithmische Algebra, 24.10.2002
•Aufgabe 2
•a) ggT(a, b mod a)
![a = 15 ; b = 2 ; Table[{{a, b - i a}, GCD[a, b - i a]}, {i, -10, 10}]](HTMLFiles/ue1_1.gif)
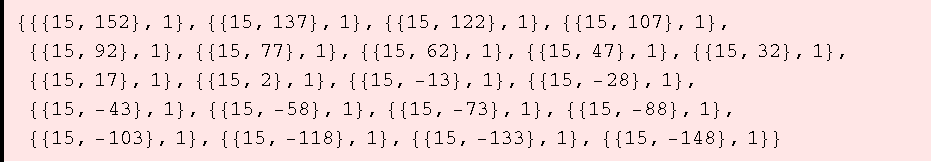
•b) ggT(a, a mod b)
![PlotGCD[a_Integer, b_Integer, k_Integer: 20, join_: False] := ListPlot[Table[GCD[a, a - i b], {i, -k, k}], PlotJoined -> join, AxesOrigin -> {k + 1, 0}, PlotRange -> All]](HTMLFiles/ue1_3.gif)
![a = 17 ; b = 2 ; GCD[a, b] PlotGCD[a, b, 20, True]](HTMLFiles/ue1_4.gif)

![[Graphics:HTMLFiles/ue1_6.gif]](HTMLFiles/ue1_6.gif)

•Aufgabe 3
![ζ[n_Integer] := Exp[π i/n]](HTMLFiles/ue1_8.gif)
![ζ[3]^3](HTMLFiles/ue1_9.gif)

![Table[ζ[3]^i, {i, 0, 6}]](HTMLFiles/ue1_11.gif)

![FList[n_Integer] := Table[(X - ζ[n] ^(2 i + 1) Y), {i, 0, n - 1}] F[n_Integer] := Simplify[Product[(X - ζ[n] ^(2 i + 1) Y), {i, 0, n - 1}]]](HTMLFiles/ue1_13.gif)
![ζ[8] FList[8] // Simplify](HTMLFiles/ue1_14.gif)

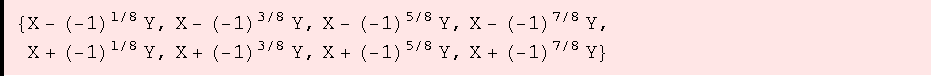
![F[3]](HTMLFiles/ue1_17.gif)

![FList[16]](HTMLFiles/ue1_19.gif)
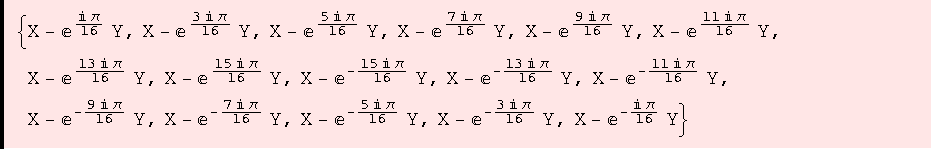
![F[16]](HTMLFiles/ue1_21.gif)

•Ideale
•Hauptideale
![ZIdeal[a_Integer, r_: 10] := Table[a i , {i, -Quotient[r, 2], Quotient[r, 2]}]](HTMLFiles/ue1_23.gif)
![ZIdeal[4]](HTMLFiles/ue1_24.gif)
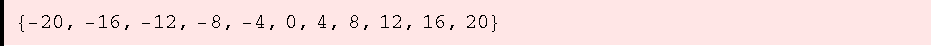
•Durchschnitt von Idealen
![ZIdeal[4, 50] ∩ ZIdeal[3, 50]](HTMLFiles/ue1_26.gif)
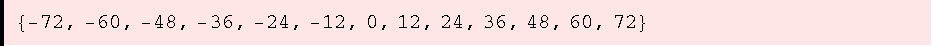
![ZIdeal[12]](HTMLFiles/ue1_28.gif)
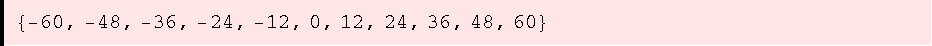
![ZIdeal[15, 50] ∩ ZIdeal[21, 50]](HTMLFiles/ue1_30.gif)

![ZIdeal[LCM[15, 21]]](HTMLFiles/ue1_32.gif)
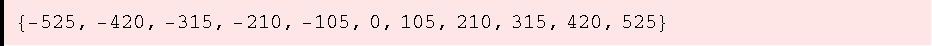
•Vereinigung
![ZIdeal[4] ∪ ZIdeal[3]](HTMLFiles/ue1_34.gif)
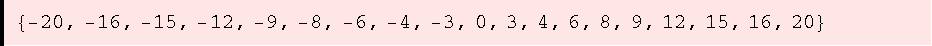
•Multiplikation
![Outer[Times, ZIdeal[5], ZIdeal[15]] // Flatten // Union](HTMLFiles/ue1_36.gif)

•Durch mehrere Elemente erzeugte Ideale
![ZIdeal[{a_Integer, b_Integer}, r_: 5] := Block[{lb = Quotient[r, 2], i, j}, Union [Flatten[Table[a i + b j , {i, -lb, lb}, {j, -lb, lb}]]] ]](HTMLFiles/ue1_38.gif)
![ZIdeal[{3, 4}]](HTMLFiles/ue1_39.gif)
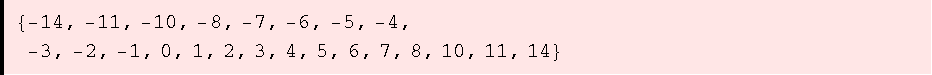
![ZIdeal[{2, 4}]](HTMLFiles/ue1_41.gif)
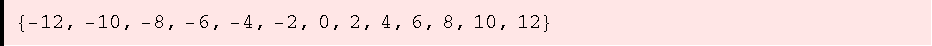
![ZIdeal[{6, 8}]](HTMLFiles/ue1_43.gif)
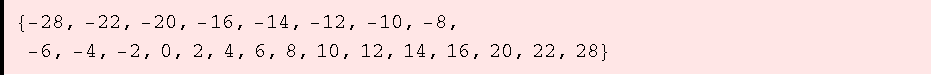
![ZIdeal[{a_Integer, b_Integer, c_Integer}, r_: 5] := Block[{lb = Quotient[r, 2], i, j, k}, Union [Flatten[Table[a i + b j + c k, {i, -lb, lb}, {j, -lb, lb}, {k, -lb, lb}]]] ]](HTMLFiles/ue1_45.gif)
![ZIdeal[{3, 4, 5}]](HTMLFiles/ue1_46.gif)
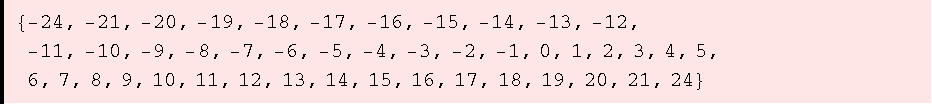
![ZIdeal[{30, 42, 54}]](HTMLFiles/ue1_48.gif)
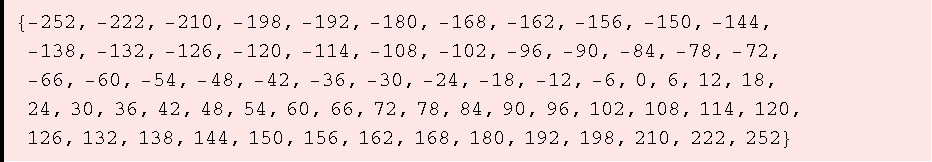
Converted by Mathematica
(November 19, 2002)
![a = 15 ; b = 2 ; Table[{{a, b - i a}, GCD[a, b - i a]}, {i, -10, 10}]](HTMLFiles/ue1_1.gif)
![a = 15 ; b = 2 ; Table[{{a, b - i a}, GCD[a, b - i a]}, {i, -10, 10}]](HTMLFiles/ue1_1.gif)
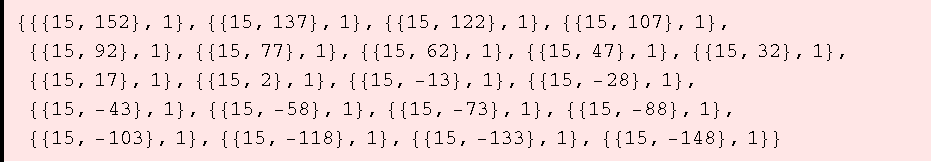
![PlotGCD[a_Integer, b_Integer, k_Integer: 20, join_: False] := ListPlot[Table[GCD[a, a - i b], {i, -k, k}], PlotJoined -> join, AxesOrigin -> {k + 1, 0}, PlotRange -> All]](HTMLFiles/ue1_3.gif)
![a = 17 ; b = 2 ; GCD[a, b] PlotGCD[a, b, 20, True]](HTMLFiles/ue1_4.gif)
![]()
![[Graphics:HTMLFiles/ue1_6.gif]](HTMLFiles/ue1_6.gif)
![]()
![]()
![]()
![]()
![]()

![FList[n_Integer] := Table[(X - ζ[n] ^(2 i + 1) Y), {i, 0, n - 1}] F[n_Integer] := Simplify[Product[(X - ζ[n] ^(2 i + 1) Y), {i, 0, n - 1}]]](HTMLFiles/ue1_13.gif)
![ζ[8] FList[8] // Simplify](HTMLFiles/ue1_14.gif)

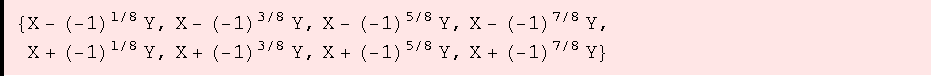
![]()
![]()
![]()
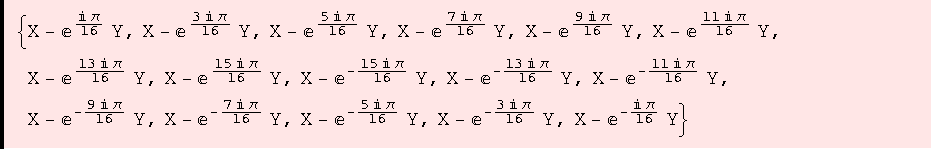
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()

![ZIdeal[{a_Integer, b_Integer}, r_: 5] := Block[{lb = Quotient[r, 2], i, j}, Union [Flatten[Table[a i + b j , {i, -lb, lb}, {j, -lb, lb}]]] ]](HTMLFiles/ue1_38.gif)
![]()
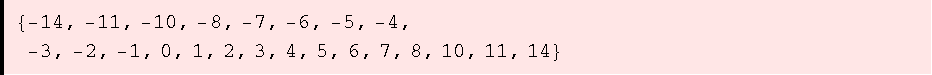
![]()
![]()
![]()
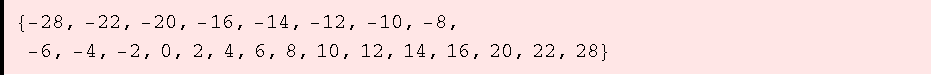
![ZIdeal[{a_Integer, b_Integer, c_Integer}, r_: 5] := Block[{lb = Quotient[r, 2], i, j, k}, Union [Flatten[Table[a i + b j + c k, {i, -lb, lb}, {j, -lb, lb}, {k, -lb, lb}]]] ]](HTMLFiles/ue1_45.gif)
![]()
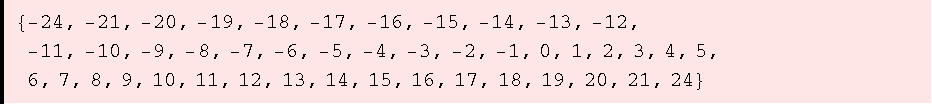
![]()